Introducción
Las matemáticas, esa ciencia abstracta, esa asignatura complicada, esa materia a veces incomprensible, esconden auténticas maravillas que algunos han olvidado y otros ni siquiera han conocido. Uno de los objetivos de este blog es mostraros esas perlas que en ocasiones permanecen ocultas a los ojos de la mayoría. Y este artículo os va a descubrir una de ellas: la fórmula de Euler.
¿Qué es un poliedro?
Un poliedro es un cuerpo geométrico en tres dimensiones cuyas caras son planas y que encierra un volumen finito. Los segmentos que unen dos caras se denominan aristas y los puntos en los que se cortan varias aristas se llaman vértices.
Podemos encontrar multitud de ejemplos de poliedros en la vida diaria:
-Una caja de zapatos,
-Un libro,
-Un balón de fútbol,
-…
-Un libro,
-Un balón de fútbol,
-…
De entre todos los poliedros hay un conjunto de ellos que es especialmente interesante: los poliedros convexos. Este tipo de poliedros cumple que para cada par de puntos que se encuentran dentro del poliedro, el segmento que los une se encuentra también dentro del mismo. Por ejemplo, una caja de zapatos

es un poliedro convexo, pero una figura de este tipo

no lo es (aunque sí es un poliedro).
Los poliedros regulares son un conjunto de poliedros convexos muy particular. Concretamente, un poliedro regular es un poliedro convexo que tiene todas sus caras iguales y sus ángulos poliédricos (ángulos formados por tres o más aristas) también iguales. Solamente existen cinco poliedros regular, de los cuales el tetraedro es el menor en lo que al número de caras se refiere. Los otros cuatro son el cubo, el octaedro, el dodecaedro y el icosaedro.
Aparte de los ya mencionados, existen multitud de tipos de poliedros: poliedros estrellados, poliedros de Catalan, sólidos arquimedianos, sólidos de Johnson, etc. Para más información sobre tipos de poliedros y sus desarrollos planos podéis descargarlos el programa Poly.
La fórmula de Euler
Tomad una caja (poliedro convexo) que tengáis en casa, por ejemplo una caja de zapatos. Contad el número de caras, aristas y vértices de la misma. Veréis que dicha caja tiene seis caras, doce aristas y ocho vértices. Ahora tomad el número de caras, restadle el número de aristas y sumadle al resultado el número de vértices. El resultado es 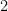 .
.
Probemos otra cosa. Cortemos un pico a la caja. Obtenemos así una cara más (para un total de 7), dos vértices más ya que desaparece uno pero aparecen tres (tenemos en total 10) y tres aristas nuevas (ahora hay 15). Realicemos la misma operación:  .
.
Dividamos ahora cualquier cara en el número de partes que queramos. Contemos ahora cuántas, caras, aristas y vértices tiene la figura obtenida. El resultado de la operación anterior es…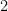 .
.
Pero dejemos ya la caja. Echad un ojo por ahí y buscad otro objeto que cumpla con la definición de poliedro convexo y realizad la misma operación: caras menos aristas más vértices. El resultado es…sí, efectivamente, 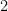 .
.
Podéis probar con cualquier cosa que tengáis en casa que sea un poliedro convexo. Siempre obtendréis el mismo resultado: 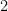 .
.
Este resultado es conocido como fórmula de Euler:
En un poliedro convexo concaras,
aristas y
vértices se cumple que:
La cantidad de figuras que cumplen la definición de poliedro convexo es tan enormemente grande que parece increíble que tengan una característica común. Este hecho tan sorprendente hace que califique a la fórmula de Euler como maravilla matemática. Y, cómo no, tuvo que ser el gran Leonhard quien nos abriera los ojos, como tantas veces.


