Probabilidad

Introducción a la probabilidad

Probabilidades

En ocasiones realizamos acciones, por ejemplo lanzar una moneda al aire, en las que conocemos de antemano los posibles resultados que se pueden dar (cara o cruz), pero no sabemos exactamente cual de ellos se va a dar.

Lo mismo ocurre cuando lanzamos un dado: sabemos que puede salir 1, 2, 3, 4, 5, o 6, pero no sabemos cual de ellos saldrá.

Los resultados de estas acciones dependen del azar:

Sabemos cuales pueden ser pero es imposible determinar de antemano cual será.

La probabilidad mide las posibilidades de que cada uno de los posibles resultados en un suceso que depende del azar sea finalmente el que se dé.

                                            Cálculo de probabilidades

Para calcular probabilidades se utiliza la siguiente fórmula:

Probabilidad = Casos favorables / Casos posibles

El resultado se multiplica por 100 para expresarlo en porcentaje.

Veamos algunos ejemplos:

a) Calcular la probabilidad de que salga "cara" al lanzar una moneda:

Casos favorables: 1 (que salga "cara")

Casos posibles: 2 (puede salir "cara" o "cruz")

Probabilidad = (1 / 2 ) * 100 = 50 %

b) Calcular la probabilidad de que salga "3" al lanzar un dado:

Casos favorables: 1 (que salga "3")

Casos posibles: 6 (puede salir "1, 2, 3, 4, 5 o 6")

Probabilidad = (1 / 6 ) * 100 = 16,6 %

c) Calcular la probabilidad de que salga "un número entre 1 y 4 " al lanzar un dado:

Casos favorables: 4 (sería válido cualquiera de los siguientes resultados "1, 2, 3, o 4")

Casos posibles: 6 (puede salir "1, 2, 3, 4, 5 o 6")

Probabilidad = (4 / 6 ) * 100 = 66,6 %

d) Calcular la probabilidad de que salga el número 76 al sacar una bolita de una bolsa con 100 bolitas numeradas del 1 al 100:

Casos favorables: 1 (sacar el número 76)

Casos posibles: 100 (hay 100 números en la bolsa)

Probabilidad = (1 / 100 ) * 100 = 1 %

e) Calcular la probabilidad de que salga "un número entre 1 y 98" al sacar una bolita de una bolsa con 100 bolitas numeradas del 1 al 100:

Casos favorables: 98 (valdría cualquier número entre 1 y 98)

Casos posibles: 100 (hay 100 números en la bolsa)

Probabilidad = (98 / 100 ) * 100 = 98 %

Diagramas en barra

Presentar datos en un gráfico de columnas

Excel para Office 365 Outlook para Office 365 Excel 2019 Outlook 2019 Excel 2016 Más...

Los gráficos de columnas resultan útiles para mostrar cambios en los datos a lo largo de un período de tiempo o para ilustrar comparaciones entre elementos. En los gráficos de columnas, las categorías suelen organizarse en torno al eje horizontal y los valores se organizan en torno al eje vertical.

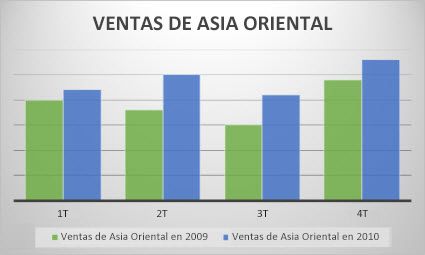
Para obtener información sobre los gráficos de columnas (y cuándo deben usarse), vea Tipos de gráficos disponibles en Office.

ExcelOutlook

Para crear un gráfico de columnas, siga estos pasos:

1. Introduzca datos en una hoja de cálculo.
2. Seleccione los datos.
3. Según la versión de Excel que esté usando, seleccione una de las siguientes opciones:
   • Excel 2016: Haga clic en Insertar, en el icono Insertar gráfico de columnas o de barras y, luego, seleccione la opción de gráfico de columnas que quiera.
     
   • Excel 2013: Haga clic en Insertar, en el icono Insertar gráfico de columnas y, luego, seleccione la opción de gráfico de columnas que quiera.
     
   • Excel 2010 y Excel 2007: Haga clic en Insertar > Columna y, luego, seleccione la opción de gráfico de columnas que quiera.
   Tiene la opción de dar un poco más de formato al gráfico. Consulte la siguiente lista para ver algunas opciones:
   Nota: Asegúrese de que hace clic en el gráfico antes de aplicar una opción de formato.
   • Para aplicar otro diseño de gráfico, haga clic en Diseño > Diseño del gráfico y seleccione un diseño.
   • Para aplicar otro estilo de gráfico, haga clic en Diseño > Estilos de gráfico y elija un estilo.
   • Para aplicar otro estilo de forma, haga clic en Formato > Estilos de forma y elija un estilo.
     Nota: Los estilos de gráfico son diferentes de los estilos de forma. Un estilo de forma es una opción de formato que se aplica solo al borde del gráfico, mientras que el estilo de gráfico es una opción de formato que se aplica a todo el gráfico.
   • Para aplicar distintos efectos de forma, haga clic en Formato > Efectos de forma y elija una opción como Bisel o Iluminado; luego, elija una subopción.
   • Para aplicar un tema, haga clic en Diseño de página > Temas y seleccione un tema.
   • Para aplicar una opción de formato a un componente específico de un gráfico (como Eje vertical (valor), Eje horizontal (categoría) o Área del gráfico, entre otros), haga clic en Formato > elija un componente del cuadro desplegable Elementos de gráfico, haga clic en Aplicar formato a la selección y realice los cambios necesarios. Repita el paso para todos los componentes que quiera modificar.
     
     Nota: Si se siente cómodo trabajando con gráficos, también puede seleccionar un área específica del gráfico, hacer clic con el botón derecho en ella y seleccionar una opción de formato.
     

¿Sabía que...?

Diagramas circulares conceptualización

Tablas de frecuencia.-

Interpretación de los gráficos:

Para poder interpretar, se debe observar: el tamaño de cada sector, el porcentaje, el color y relacionar entre ellos para saber cual es el mayor, el menor, la suma de los menores cuanto alcanza, etc. etc. 

Diagramas circulares

Convertir porcentajes en fracciones

Para convertir un porcentaje en una fracción sigue estos pasos:

Paso 1: escribe el porcentaje dividido entre 100.

Paso 2: Si el porcentaje no es un número entero, multiplica arriba y abajo por 10 una vez por cada cifra después del punto decimal. Por ejemplo, si hay un número después del decimal multiplica por 10, si hay dos multiplica por 100, etc.

Paso 3: Simplifica (o reduce) la fracción

Ejemplo 1: Expresa 75% en forma de fracción

Paso 1: Escribe:

75

100

Paso 2: el porcentaje es un número entero, así que no hacemos nada en este paso.

Paso 3: simplifica la fracción:

÷ 25
75	=	3
100		4
÷ 25

Respuesta = 3/4

Nota: 75/100 es una fracción decimal y 3/4 es una fracción común

Ejemplo 2: expresa 62.5% en forma de fracción

Paso 1: escribe:

62.5

100

Paso 2: multiplica arriba y abajo por 10 (porque hay 1 cifra decimal)

	× 10
62.5	=	625
100		1,000
	× 10

(¿Ves cómo arriba queda un simple número entero?)

Paso 3: simplifica la fracción (a mí me ha llevado dos pasos, ¡igual tú lo haces en uno!):

	÷ 25		÷ 5
625	=	25	=	5
1,000		40		8
	÷ 25		÷ 5

Respuesta = 5/8

 

Ejemplo 3: expresa 150% en forma de fracción

Paso 1: escribe:

150

100

Paso 2: el porcentaje es un número entero, así que el paso 2 no hace falta.

Paso 3: simplifica la fracción (lo hice en un paso):

	÷ 50
150	=	3
100		2
	÷ 50

Respuesta = 3/2

(y es igual a 1½, lee fracciones mixtas)

Introducción a porcentajes

Círculo

Elementos de un círculo

1) Centro: es un punto interior equidistante de todos los puntos de la circunferencia.

2) Radio: es un segmento que une el centro con un punto de la circunferencia.

3) Diámetro: es el mayor segmento que une dos puntos de la circunferencia. Corresponde al doble del radio.

4) Arco: es un segmento curvilíneo de puntos que pertenecen a la circunferencia.

5) Cuerda: es un segmento que une dos puntos de la circunferencia. Las cuerdas con mayor longitud que podemos encontrar son los diámetros.

6) Secante: es una recta que corta la circunferencia en dos puntos.

7) Tangente: es una recta que toca la circunferencia en un solo punto.

Calculo del perimetro y área de un circulo

Conceptualización de proporcionalidad directa e inversa

Proporción directa

Diremos que la proporción es directa si relacionan magnitudes en las que al aumentar una también lo hace la otra y viceversa.

En este caso la regla de tres se aplicará de la siguiente manera:

Ejemplo

Si un tren tarda  horas en recorrer  kilómetros, ¿cuánto tardará en recorrer el doble?

Primero observamos que es un caso de proporción directa ya que a más horas mas kilómetros recorrerá el tren. La respuesta se puede deducir mentalmente, puesto que si el tren tiene que recorrer el doble de distancia también tardará el doble de tiempo, con lo que necesitará h para recorrer los km. La deducción es correcta, pero veamos como se resuelve aplicando la regla de tres para proporciones directas.

Tenemos la siguiente relación:

Es decir, si en  h se recorren km, en  h se recorrerán .

Observamos que la relación también puede expresarse siguiendo el modelo de igualdad entre fracciones usado para describir el concepto de proporción:

Donde las dos magnitudes del ejercicio quedan en fracciones distintas: el tiempo a un lado de la igualdad y la distancia al otro.

Ahora sólo hay que despejar  para hallar la solución:

Por tanto el tren tardará  horas en recorrer km.

Ejemplo

Si el kilo de cerezas va a  €, ¿cuánto costará comprar medio kilo?

Tenemos una proporcionalidad directa puesto que a menos kilos que compremos más barato nos costará.

Tenemos la relación de proporcionalidad:

Aplicando la regla de tres tenemos:

€

Es decir, medio kilo de cerezas costarán la mitad que un kilo.

Proporción inversa

Diremos que la proporción es inversa si implica una relación de magnitudes en que al aumentar una la otra disminuye y viceversa. En este caso la regla de tres se aplicará de la siguiente manera:

Ejemplo

Si  agricultores tardan  días en arar un campo, ¿cuánto tardarán agricultores en realizar el mismo trabajo?

Se trata claramente de un ejemplo de proporción inversa, puesto que a más agricultores trabajando menos tiempo se tardará en arar el mismo campo.

Para resolverlo se aplica la regla de tres como se ha enseñado:

Y se resuelve:

días

Es decir, mientras que dos agricultores tardan  días, con la ayuda de otros compañeros consiguen hacer el mismo trabajo en tan solo  días